Freebase percentage AND pH calculator

[Infundibulum]

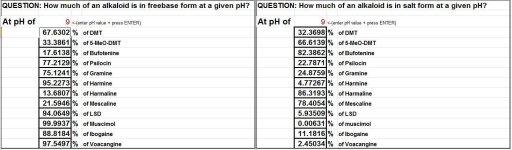
Hi all,

SWIM made a small Excel document (see snapshot) which calculates the percentage of an alkaloid that is in its freebase form at a certain pH given that its pKa is known. The applet is horrid since SWIM's not a programmer. Should anyone desires, feel free to develop a better applet for it.

This Excel programme is for mostly for curiosity and entertainment purposes. Playing around with it people can see how gradual increases/decreases of the pH affect the amount of alkaloids in freebase form.

But it can be a useful tool as well; say that someone wants to selectively precipitate harmine (pKa=7.7) out of harmaline(pKa=9.8 ) out of a solution. Which is the best pH value where he will precipitate most of the harmine out and the least amount of harmine?

SWIM plotter a graph showing freebase harmine depletion/precipitation (that equals harmine salt left in solution, blue line) versus freebase harmaline accumulatio (pink line).

The intersection point corresponds at a pH of around 8.75, which is the pH where one will get the most harmine with the least harmaline contamination. At this pH one will in theory get at around 92% harmine and 8% harmaline in his precipitates.

From the graph one can also see that at pH of around 8 one will get only minimal harmaline contamination, yet he will only precipitate roughly 68% of the harmine.

EDIT:
A small disclaimer for the use of these equations.

1) In theory, theory and practise are the same, but in practise they are not. That is to say that all these equations are purely theoretical. In real life things might be (and often are) a bit different.

2) The equations give a very simple result. Simply the amount of the alkaloid that exists in freebase and salt form. It does not imply anything about precipitation, solubility etc.

3) The results of these equations are more realistic the more pure the preparation of an alkaloid is. An alkaloid present in a crude solution with other crap may behave differently. A relatively pure alkaloid however is more likely to behave as the equations predict.

 

[The Traveler]

Very cool of you Infundibulum!

I'll make an web-app out of this so we can all use it online.
Any other calculation that I can add to this online calculator program?


Kind regards,

The Traveler

 

[Infundibulum]

We could also add a pH calculator for acids and bases in the applet to answer questions like: what pH you get if you dissolve x amount g of x, y, z acid/base in x ml of water of water?

There are already such online calculators but they do not usually include acids like citric acid, tartaric acid, fumaric acid or bases like sodium carbonate and sodium bicarbonate.

 

[The Traveler]

That would be really useful to include in our online calculator. Can you provide the formulas for that?

And maybe it's a good idea to make a pKa 0 list of our favorite molecules?

 

[Infundibulum]

I'll do that for as many acids and bases I can find. It will take some time though since weak acids and bases have tricky calculations!

 

[acolon_5]

That is very, very cool.

I can see this being useful in so many different extractions.

Will you be doing this for other molecules, or will this work for all of them? I really don't know that much about chem, sorry...

 

[Infundibulum]

Re to Acolon: The calculator works with any alkaloid, given that its pKa is known. Hope that explains it!

Now SWIM's preparing some equations for the calculation of the pH when x grams of an acid/base are added in x ml of water.

What he has in his list so far is acetic acid, fumaric acid, citric acid, hydrochloric acid, sulphyric acid, (from the acids part) and sodium carbonate, sodium bicarbonate, NaOH, KOH, CaOH

Please tell him if you'd like any other substance to be included in the calculator

 

[The Traveler]

What about Phosphoric acid?

Re to Acolon: The calculator works with any alkaloid, given that its pKa is known. Hope that explains it!

Now SWIM's preparing some equations for the calculation of the pH when x grams of an acid/base are added in x ml of water.

What he has in his list so far is acetic acid, fumaric acid, citric acid, hydrochloric acid, sulphyric acid, (from the acids part) and sodium carbonate, sodium bicarbonate, NaOH, KOH, CaOH

Please tell him if you'd like any other substance to be included in the calculator

 

[acolon_5]

Re to Acolon: The calculator works with any alkaloid, given that its pKa is known. Hope that explains it!

Now SWIM's preparing some equations for the calculation of the pH when x grams of an acid/base are added in x ml of water.

What he has in his list so far is acetic acid, fumaric acid, citric acid, hydrochloric acid, sulphyric acid, (from the acids part) and sodium carbonate, sodium bicarbonate, NaOH, KOH, CaOH

Please tell him if you'd like any other substance to be included in the calculator

It does, thank you....again WONDERFUL idea.

And yeah, phosphoric acid.... I use that alot both in my aya brews as well as in extractions, I think that's about it.

 

[Infundibulum]

The pH calculator is ready (attached). Again, it is in a Excel document, if the Traveler can put them in some nice-looking applet that would be wonderful. There are some important notes re to this calculator and how it can be used correctly:

1) This calculator does NOT make the most absolute calculations about pH. The formulas it uses contain some assumptions for simplicity's sake that have minimal impact from a practical standpoint.

2) The pH of an acid or base is dependent on the amount of acid dissolved in a certain amount of water. The calculator uses these values to calculate the pH. pH is however dependent on the temperature as well. The values the calculator returns are the pH values if the solution is at 25 C (77 F).

3) All amounts are in grams. Some substances like hydrochloric acid and ammonia are gases while others like acetic acid, sulphuric acid and ammonia are liquids in their pure form. The above substances are most commonly sold dissolved in water with a "%" concentration given. For instance, acetic acid can be sold as vinegar that contains 5% acetic acid. This means that 5g of pure acetic acid are present in every 100 of vinegar. The pH of a 5% vinegar would be 2.419.

Similarly, a 10% of hydrochloric acid has a pH of -0.438 according to the calculator. If one dilutes 10 times this hydrochloric acid he's going to have a 1% hydrochloric acid solution. The pH will be 0.561.

4) All the pH calculations are for "pure" solutions of water and acid/base. Other materials (such as plant material) added to the acidic/basic solution(s) will change the pH to some extend since they contain small amounts of acids, bases and salts.

Have good fun with the calculator!

 

[The Traveler]

Thank you very much Infundibulum!

You will be noticed when the online aplication is ready.

 

[69ron]

Experience has shown those types of calculations to actually be wrong for a lot of alkaloids because their solubility as freebase being lower than their solubility as a salt messes up the calculation.

You will find it inaccurate for most alkaloids, especially harmine and harmaline because their freebase is insoluble in water and that dramatically alters the calculation, and also makes the pKa a little bit irrelevant. I’m sure you could make it more accurate if you somehow added solubility to the calculation, but I have no idea how to do that.

 

[Infundibulum]

Experience has shown those types of calculations to actually be wrong for a lot of alkaloids because their solubility as freebase being lower than their solubility as a salt messes up the calculation.

You will find it inaccurate for most alkaloids, especially harmine and harmaline because their freebase is insoluble in water and that dramatically alters the calculation, and also makes the pKa a little bit irrelevant. I’m sure you could make it more accurate if you somehow added solubility to the calculation, but I have no idea how to do that.

This is a fair concern; a factor that is is not taken into account in the equations is that the insolubility of some freebase forms may act as a sink, thus leading to gradual depletion of the rest of the alkaloids.

SWIM finds that the notion of "sink" albeit intuitive it is not necessarily true; the reason for this is because the insolubility of the freebase forms is not a real "sink". It would be a real sink if the precipitates were not able to interact with the solution any more. We know that this is not the case. Precipitated water-insoluble alkaloids will interact with the solution to reach at a balance if salt vs freebase form.

As an example of the above, SWIM has been unable to precipitate all of the dmt from a solution pH = 9 if just left to sit for a couple of days. Maybe all would have precipitated if he had waited for 2 weeks though. Addition of more base resulted in more precipitations.

The equations are not 100% accurate. They are fairly accurate to the best ou our knowledge and a useful guide for extraction.

 

[69ron]

SWIM has a lot of experience using pKa as a starting point in such things and has found wide variances in this equation for different alkaloids. With some alkaloids you can freebase all the alkaloids below the pKa, with others (like DMT) you cannot. Every alkaloid SWIM has experience with behaves differently.

These mathematic equations are great starting points, but they are usually inaccurate. SWIM found this particular pKa equation is always inaccurate. It’s too simplistic. The solubility of the alkaloid as freebase or as salt has a big impact on this. For example, 50% of the DMT doesn’t crash out at its pKa, none does, at least not at first. After many days some does crash out. The problem is even worse for bufotenine because it’s very water soluble as freebase and this effects the solution because as freebase it’s still part of the solution. SWIM has never seen bufotenine crash out at it’s pKa, even after many weeks. Mescaline has the same problem.

 

[Infundibulum]

SWIM has a lot of experience using pKa as a starting point in such things and has found wide variances in this equation for different alkaloids. With some alkaloids you can freebase all the alkaloids below the pKa, with others (like DMT) you cannot. Every alkaloid SWIM has experience with behaves differently.

These mathematic equations are great starting points, but they are usually inaccurate. SWIM found this particular pKa equation is always inaccurate. It’s too simplistic. The solubility of the alkaloid as freebase or as salt has a big impact on this. For example, 50% of the DMT doesn’t crash out at its pKa, none does, at least not at first. After many days some does crash out. The problem is even worse for bufotenine because it’s very water soluble as freebase and this effects the solution because as freebase it’s still part of the solution. SWIM has never seen bufotenine crash out at it’s pKa, even after many weeks. Mescaline has the same problem.

SWIM does not really understand what SWIY is saying; The equation gives the amount of freebase alkaloid versus the salted at different pHs. Nothing more and nothing less. The same equation is used for calculating the pKa in the first place by the chemists! They ACTUALLY find the pH at which 50% of the alkaloid is in freebase and 50% in salt. and they use much more sophisticated techniques than precipitation.

It is as simple as that. Simple, because it does not tell anything about solubilities or anything like that because it does not intend to do that. But it is not simplistic. Just simple.

 

[benzyme]

Marvin Sketch (free) has a pKa calculator

here's one I plugged in for mescaline. the first column of numbers is the pH, the second is % of species 1, and the third is % of species 2.

 

[69ron]

SWIM has a lot of experience using pKa as a starting point in such things and has found wide variances in this equation for different alkaloids. With some alkaloids you can freebase all the alkaloids below the pKa, with others (like DMT) you cannot. Every alkaloid SWIM has experience with behaves differently.

These mathematic equations are great starting points, but they are usually inaccurate. SWIM found this particular pKa equation is always inaccurate. It’s too simplistic. The solubility of the alkaloid as freebase or as salt has a big impact on this. For example, 50% of the DMT doesn’t crash out at its pKa, none does, at least not at first. After many days some does crash out. The problem is even worse for bufotenine because it’s very water soluble as freebase and this effects the solution because as freebase it’s still part of the solution. SWIM has never seen bufotenine crash out at it’s pKa, even after many weeks. Mescaline has the same problem.

SWIM does not really understand what SWIY is saying; The equation gives the amount of freebase alkaloid versus the salted at different pHs. Nothing more and nothing less. The same equation is used for calculating the pKa in the first place by the chemists! They ACTUALLY find the pH at which 50% of the alkaloid is in freebase and 50% in salt. and they use much more sophisticated techniques than precipitation.

It is as simple as that. Simple, because it does not tell anything about solubilities or anything like that because it does not intend to do that. But it is not simplistic. Just simple.

The original post implies this can be used to separate harmine from harmaline and it DOES NOT WORK LIKE THAT. The reason is that the solution contains not just harmine. The pKa is calculated using pure harmine and pure water. The presence of the harmaline and other impurities affects it quite a lot.

Try it using a microscope and you'll see what I'm talking about. The two crystals look very different and are easy to identify with a microscope. You'll find the results do not match that calculation because it's too simplistic. It doesn't take into account the presence of the harmaline and other impurities, which through the whole thing off.

On paper this looks good, but in reality it's not that simple. Test it in the real world with a rue extract that contains harmine, harmaline, harmalol, and a bunch of other crap.

 

[Infundibulum]

SWIM feels that SWIY is shifting goalposts and changing the argument all over.

SWIM is not going into an argument of whether the predicted pH of 8.75 is the ideal pH to precipitate harmine out of harmaline from crude solutions. It is a good guide however when relatively pure preparations of both alkaloids are used. And yes, impurities present can throw the theoretical predictions out.

I will add a few notes explicitly stating:

1) that the equations are all theoretical and
2) the implications one has to consider when using the results of these equations for practical reasons.

I hope this will resolve the debate!

 

[69ron]

I'm honestly not shifting my argument. I saw that you were not really understanding what I was saying so I came at it from a different angle. I think you get what I'm saying now. While this works for pure alkaloids, in the real world with impure extracts, the other elements in the mix mess it up.

 

[Infundibulum]

I'm honestly not shifting my argument. I saw that you were not really understanding what I was saying so I came at it from a different angle. I think you get what I'm saying now. While this works for pure alkaloids, in the real world with impure extracts, the other elements in the mix mess it up.

Yup!