Hello Nexus. After finishing my physics PhD, I took some time to hunt a wild TOE while pulling together a collection of interactive physics apps that I had been working on. The collection grows much slower than my list of ideas, so perhaps this has to be a lifelong project. 
For now I'm creating this thread to open the project to criticism and suggestions, but also because you can only think so far with one mind.
My philosophy is that the best way to learn about physics is through direct interaction. i.e. Seeing is believing. There are physicists who claim to be experts in certain principles but don't know what the relevant interactions look like. In fact they insist that you can't understand complicated physics without learning their restrictive language. I always knew they were wrong because I could see the physics in my head. I created each of these apps to explore particular mathematical principles in a way that I thought might be entertaining/educational even for people with no technical background. These principles are unique yet interconnected.
That being said, there are as many unreleased apps that simply aren't polished enough, and there is still so much that I haven't figured out how to write in terms of code...or math, for that matter, but I have to invent my own. Polyphys has been my temple for a while now, and it will continue to expand indefinitely. The TOE is coming along slowly but surely, and I'm actually going a bit crazy ever since I started imagining a connection between the mathematical concepts and ancient religions, but that's another story.
I will answer the obvious question.
What's the TOE?
Imagine an electromagnetic pulse bouncing back and forth in a cavity. Every time the pulse reflects off one side of the cavity, it changes direction. To an observer, it looks like the pulse is either travelling to the left or right, depending on which side is reflected off last, but the pulse also has a sort of "self" perspective, in which it sees itself as always pushing forward. Thus, every time an observer sees the pulse reflect and change direction, we can instead imagine the pulse's persective by "unfolding" the cavity, so that the reflected/bent path becomes straightened out.
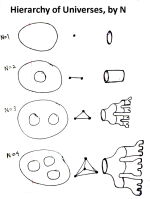
This (a cavity with only 2 walls) is what I call the N=2 universe of interactions (pic). It specifies how a system is able to evolve if it can be conformally mapped (through topological surgery) to a set of 2 points... The path isn't actually that interesting, really, but it becomes more interesting when we consider the N=3 pathways: With three points, helical modes emerge. These allow forward and backward time to be differentiated, but the harder aspect of this geometry is that the 3-point path is represented by a sequence of binary choices, so that the "unfolded" version of this cavity looks like a tree. This is, in some sense, the "worldline" of a particle in our universe. The effect of increasing the order of the interaction from N=2 to N=3 is that the topology of the particle worldline is changed drastically from a simple tube to a binary tree.
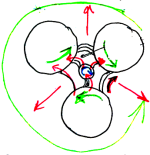
The N=3 tree can then be sliced up and connected back on itself in a particular way to derive a 5-dimensional shape (pic). The shape has various cycles connected by special ratios that I am still struggling to understand, but ultimately I suspect that some harmonic coupling enforced by topology (which we can classify more easily by taking extreme limits) can be used to model fundamental particles in a way that elegantly synthesizes EM charge (the green/red cycles in previous pic) and gravitational mass (the central blue cycle) via the fundamenal interlinkings of the N=1-4 interaction spaces.
And the other obvious question.
What is the connection to ancient religions?
The early humans discovered the natural numbers: 1,2,3,etc. The algebraic properties of these numbers are innate.
Imagine what they must have thought of these objects that exist simultaneously out in the world and in the mind. Early humans would have seen them as mystical objects. The algebraic properties of the integers would have seemed like pure magic. Inevitably, they created cults worshiping the different numbers. These number cults eventually morphed into ancient religions, and ultimately into modern religions.
The magic is in the archetypes. It's not a coincidence that certain truths will ring true periodically for the rest of time. This is because there is an underlying mathematical mechanism. There are certain repeating patterns in the interactions between integers themselves, so any system referring to an integer number of things will inherit the dynamical properties of the corresponding integer...

For now I'm creating this thread to open the project to criticism and suggestions, but also because you can only think so far with one mind.
My philosophy is that the best way to learn about physics is through direct interaction. i.e. Seeing is believing. There are physicists who claim to be experts in certain principles but don't know what the relevant interactions look like. In fact they insist that you can't understand complicated physics without learning their restrictive language. I always knew they were wrong because I could see the physics in my head. I created each of these apps to explore particular mathematical principles in a way that I thought might be entertaining/educational even for people with no technical background. These principles are unique yet interconnected.
That being said, there are as many unreleased apps that simply aren't polished enough, and there is still so much that I haven't figured out how to write in terms of code...or math, for that matter, but I have to invent my own. Polyphys has been my temple for a while now, and it will continue to expand indefinitely. The TOE is coming along slowly but surely, and I'm actually going a bit crazy ever since I started imagining a connection between the mathematical concepts and ancient religions, but that's another story.
I will answer the obvious question.
What's the TOE?
Imagine an electromagnetic pulse bouncing back and forth in a cavity. Every time the pulse reflects off one side of the cavity, it changes direction. To an observer, it looks like the pulse is either travelling to the left or right, depending on which side is reflected off last, but the pulse also has a sort of "self" perspective, in which it sees itself as always pushing forward. Thus, every time an observer sees the pulse reflect and change direction, we can instead imagine the pulse's persective by "unfolding" the cavity, so that the reflected/bent path becomes straightened out.
This (a cavity with only 2 walls) is what I call the N=2 universe of interactions (pic). It specifies how a system is able to evolve if it can be conformally mapped (through topological surgery) to a set of 2 points... The path isn't actually that interesting, really, but it becomes more interesting when we consider the N=3 pathways: With three points, helical modes emerge. These allow forward and backward time to be differentiated, but the harder aspect of this geometry is that the 3-point path is represented by a sequence of binary choices, so that the "unfolded" version of this cavity looks like a tree. This is, in some sense, the "worldline" of a particle in our universe. The effect of increasing the order of the interaction from N=2 to N=3 is that the topology of the particle worldline is changed drastically from a simple tube to a binary tree.
The N=3 tree can then be sliced up and connected back on itself in a particular way to derive a 5-dimensional shape (pic). The shape has various cycles connected by special ratios that I am still struggling to understand, but ultimately I suspect that some harmonic coupling enforced by topology (which we can classify more easily by taking extreme limits) can be used to model fundamental particles in a way that elegantly synthesizes EM charge (the green/red cycles in previous pic) and gravitational mass (the central blue cycle) via the fundamenal interlinkings of the N=1-4 interaction spaces.
And the other obvious question.
What is the connection to ancient religions?
The early humans discovered the natural numbers: 1,2,3,etc. The algebraic properties of these numbers are innate.
Imagine what they must have thought of these objects that exist simultaneously out in the world and in the mind. Early humans would have seen them as mystical objects. The algebraic properties of the integers would have seemed like pure magic. Inevitably, they created cults worshiping the different numbers. These number cults eventually morphed into ancient religions, and ultimately into modern religions.
The magic is in the archetypes. It's not a coincidence that certain truths will ring true periodically for the rest of time. This is because there is an underlying mathematical mechanism. There are certain repeating patterns in the interactions between integers themselves, so any system referring to an integer number of things will inherit the dynamical properties of the corresponding integer...